爬楼梯、青蛙跳系列

70. 爬楼梯 - 力扣（LeetCode）

解题思路：
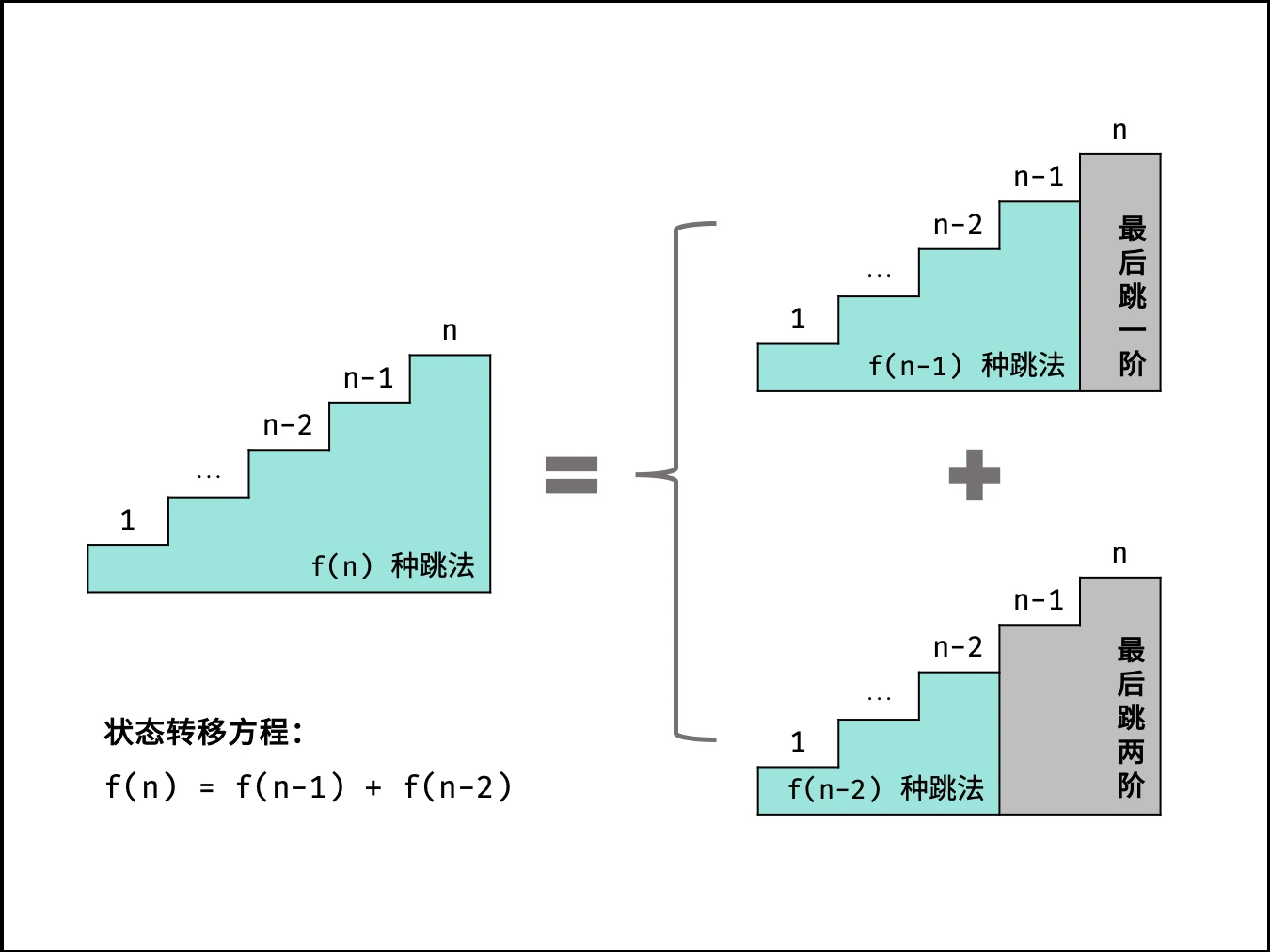
设跳上 n 级台阶有 f(n)种跳法。在所有跳法中，青蛙的最后一步只有两种情况： 跳上 1 级或 2 级台阶。

当为 1 级台阶： 剩 n−1个台阶，此情况共有 f(n−1) 种跳法。
当为 2 级台阶： 剩 n−2个台阶，此情况共有f(n−2)种跳法。
即 f(n)为以上两种情况之和，即f(n)=f(n−1)+f(n−2) ，以上递推性质为斐波那契数列。
因此，本题可转化为 求斐波那契数列的第 n项，区别仅在于初始值不同：

• 青蛙跳台阶问题： f(0)=1 , f(1)=1 , f(2)=2。
• 斐波那契数列问题： f(0)=0, f(1)=1f(1)=1, f(2)=1 。

class Solution {
    public int climbStairs(int n) {
        int a = 1, b = 1, sum;
        for(int i = 0; i < n - 1; i++){
            sum = a + b;
            a = b;
            b = sum;
        }
        return b;
    }
}
复制

ACM：

import java.util.Scanner;

public class Solution {
    public static int climbStairs(int n) {
        int a = 1, b = 1, sum;
        for (int i = 0; i < n - 1; i++) {
            sum = a + b;
            a = b;
            b = sum;
        }
        return b;
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int result = climbStairs(n);
        System.out.println(result);
        scanner.close();
    }
}

复制