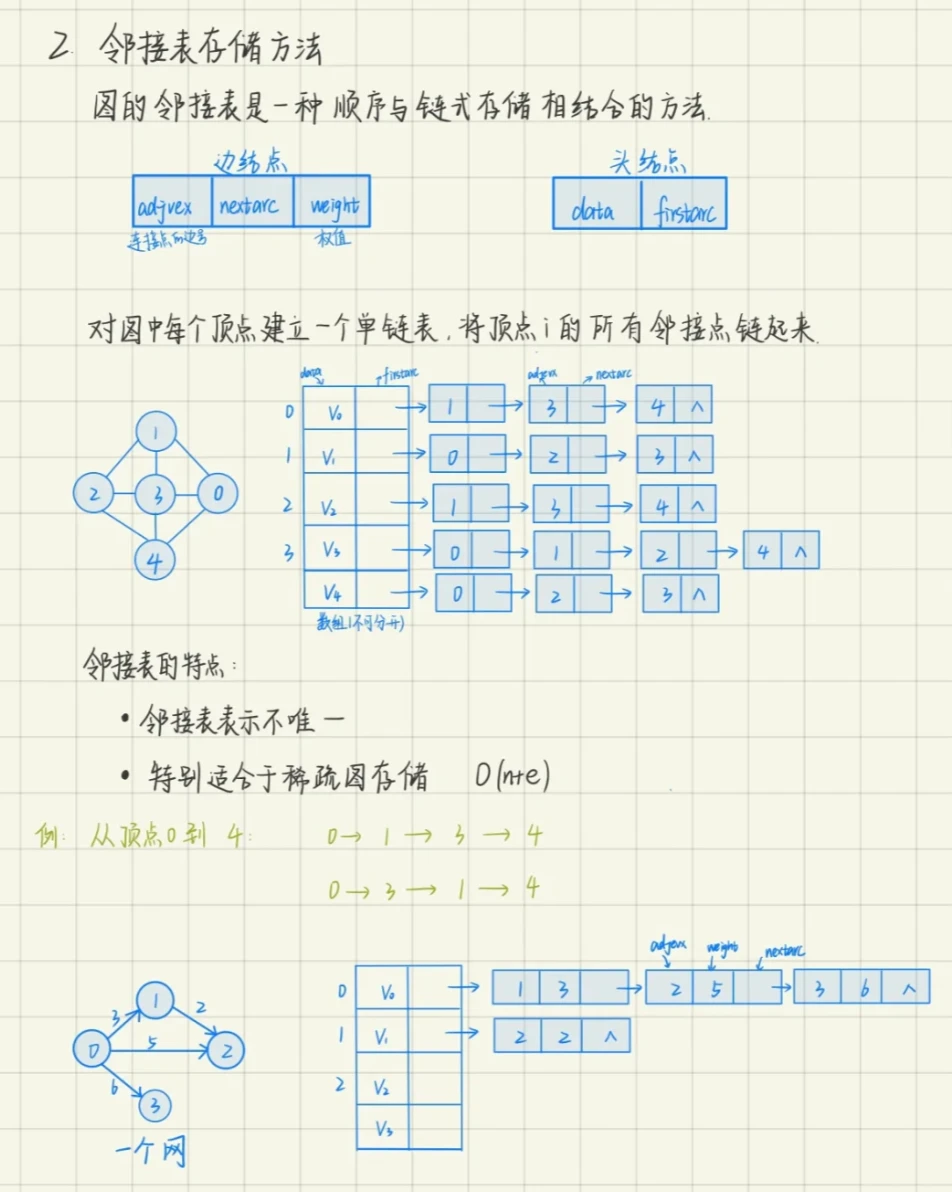
数组
数组是非常基础的数据结构,在面试中,考察数组的题目一般在思维上都不难,主要是考察对代码的掌控能力
一维数组在内存空间中是连续的
数组是存放在连续内存空间上的相同类型数据的集合。
数组可以方便的通过下标索引的方式获取到下标下对应的数据。
举一个字符数组的例子,如图所示:
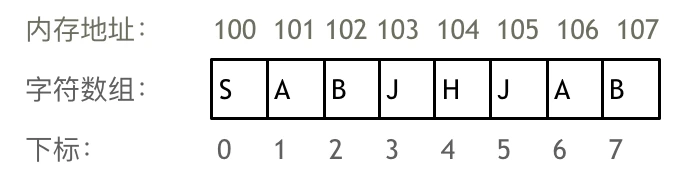
需要两点注意的是
- 数组下标都是从0开始的。
- 数组内存空间的地址是连续的
正是因为数组的在内存空间的地址是连续的,所以我们在删除或者增添元素的时候,就难免要移动其他元素的地址。
例如删除下标为3的元素,需要对下标为3的元素后面的所有元素都要做移动操作,如图所示:
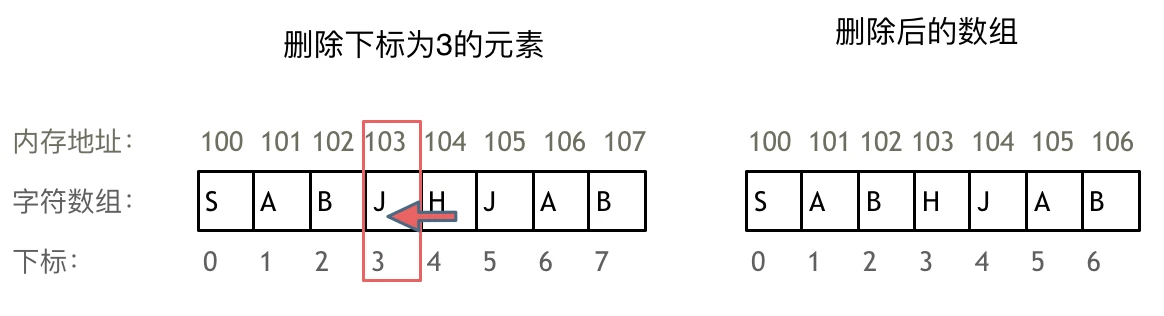
而且大家如果使用C++的话,要注意vector 和 array的区别,vector的底层实现是array,严格来讲vector是容器,不是数组。
数组的元素是不能删的,只能覆盖。
那么二维数组直接上图,大家应该就知道怎么回事了
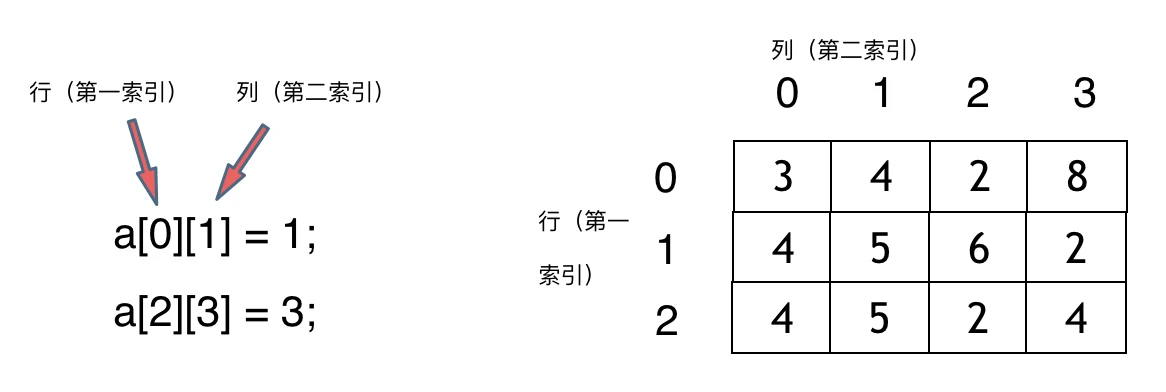
那么二维数组在内存的空间地址是连续的么?
C++
不同编程语言的内存管理是不一样的,以C++为例,在C++中二维数组是连续分布的。
我们来做一个实验,C++测试代码如下:
void test_arr() {
int array[2][3] = {
{0, 1, 2},
{3, 4, 5}
};
cout << &array[0][0] << " " << &array[0][1] << " " << &array[0][2] << endl;
cout << &array[1][0] << " " << &array[1][1] << " " << &array[1][2] << endl;
}
int main() {
test_arr();
}
测试地址为
0x7ffee4065820 0x7ffee4065824 0x7ffee4065828
0x7ffee406582c 0x7ffee4065830 0x7ffee4065834
注意地址为16进制,可以看出二维数组地址是连续一条线的。
一些录友可能看不懂内存地址,我就简单介绍一下, 0x7ffee4065820 与 0x7ffee4065824 差了一个4,就是4个字节,因为这是一个int型的数组,所以两个相邻数组元素地址差4个字节。
0x7ffee4065828 与 0x7ffee406582c 也是差了4个字节,在16进制里8 + 4 = c,c就是12。
如图:
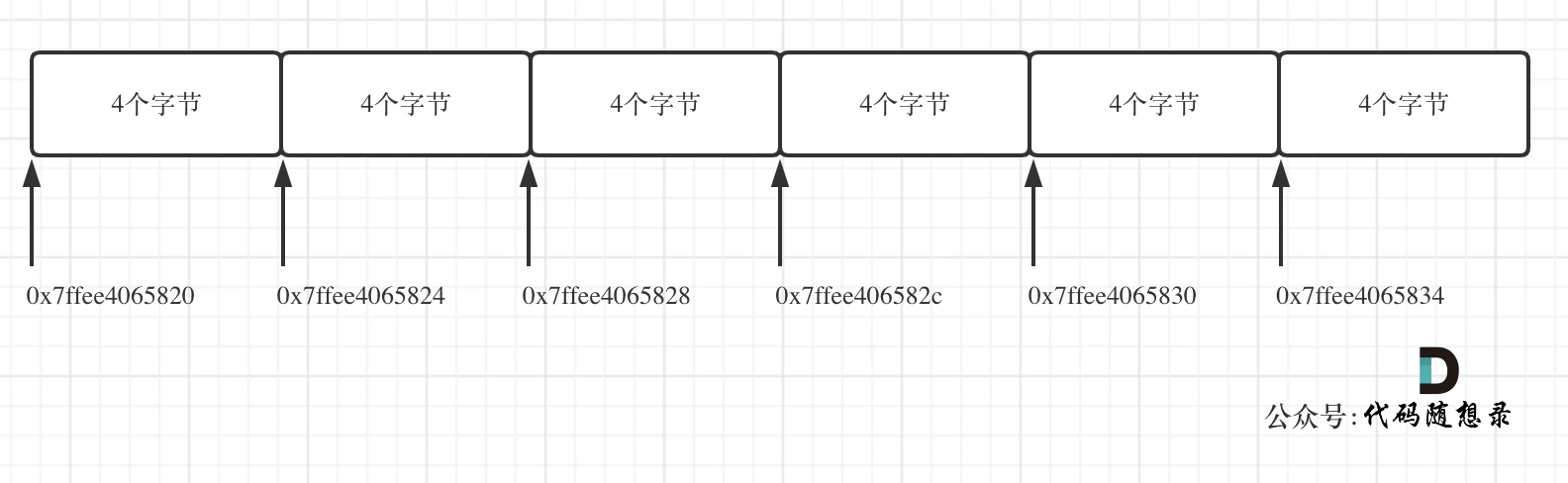
所以可以看出在C++中二维数组在地址空间上是连续的。
Java
像Java是没有指针的,同时也不对程序员暴露其元素的地址,寻址操作完全交给虚拟机。
所以看不到每个元素的地址情况,这里我以Java为例,也做一个实验。
public static void test_arr() {
int[][] arr = {{1, 2, 3}, {3, 4, 5}, {6, 7, 8}, {9,9,9}};
System.out.println(arr[0]);
System.out.println(arr[1]);
System.out.println(arr[2]);
System.out.println(arr[3]);
}
输出的地址为:
[I@7852e922
[I@4e25154f
[I@70dea4e
[I@5c647e05
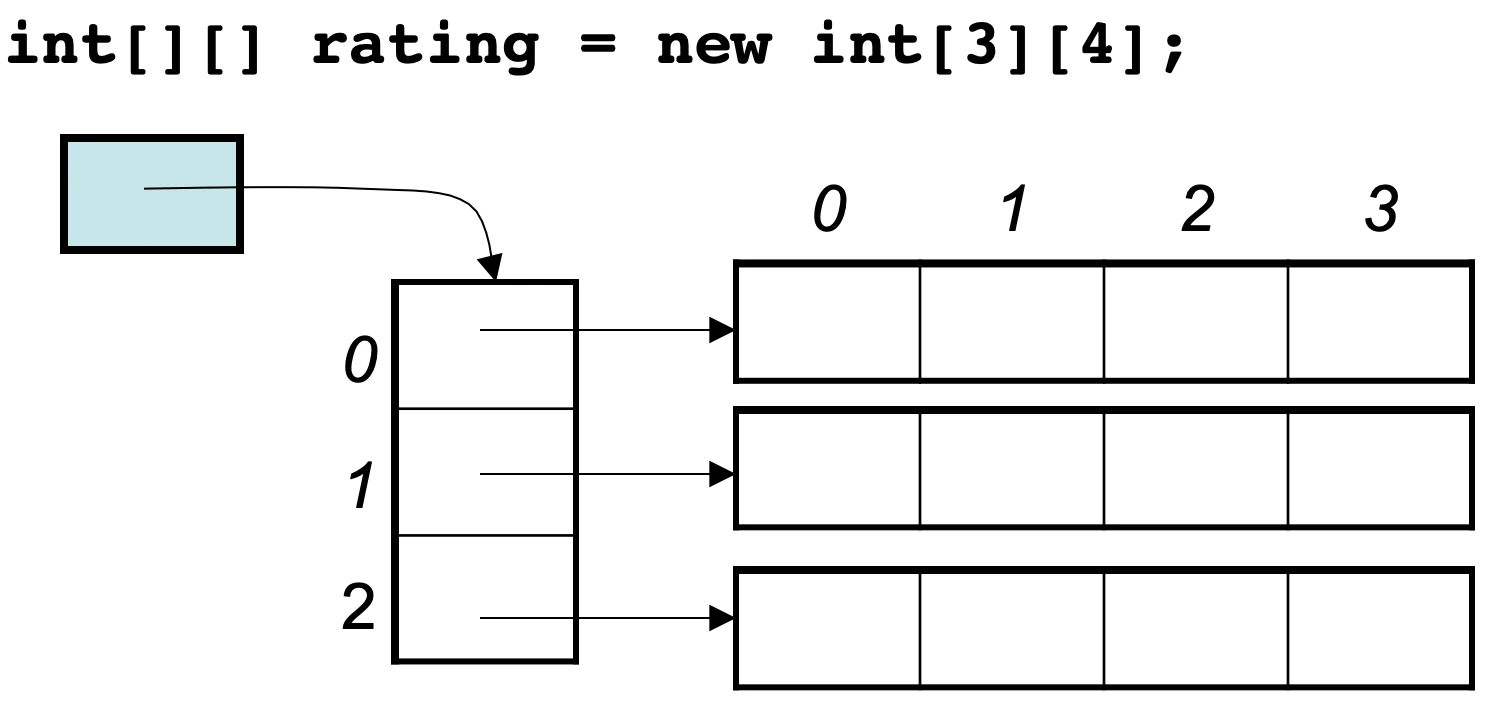
这里的数值也是16进制,这不是真正的地址,而是经过处理过后的数值了,我们也可以看出,二维数组的每一行头结点的地址是没有规则的,更谈不上连续。
所以Java的二维数组可能是如下排列的方式:
链表
什么是链表,链表是一种通过指针串联在一起的线性结构,每一个节点由两部分组成,一个是数据域一个是指针域(存放指向下一个节点的指针),最后一个节点的指针域指向null(空指针的意思)。
链表的入口节点称为链表的头结点也就是head。
如图所示: 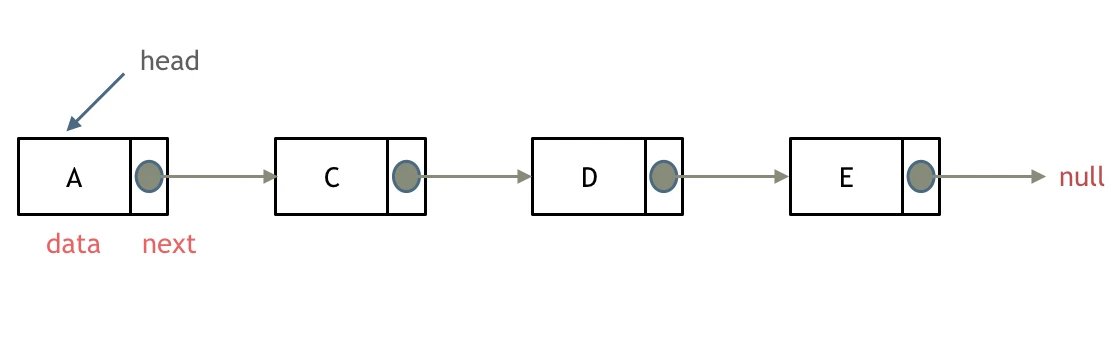
链表的类型
接下来说一下链表的几种类型:
单链表
刚刚说的就是单链表。
双链表
单链表中的指针域只能指向节点的下一个节点。
双链表:每一个节点有两个指针域,一个指向下一个节点,一个指向上一个节点。
双链表 既可以向前查询也可以向后查询。
如图所示: 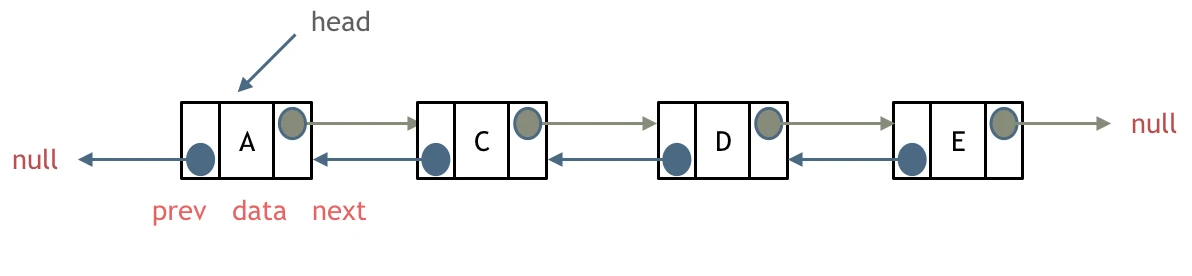
循环链表
循环链表,顾名思义,就是链表首尾相连。
循环链表可以用来解决约瑟夫环问题。
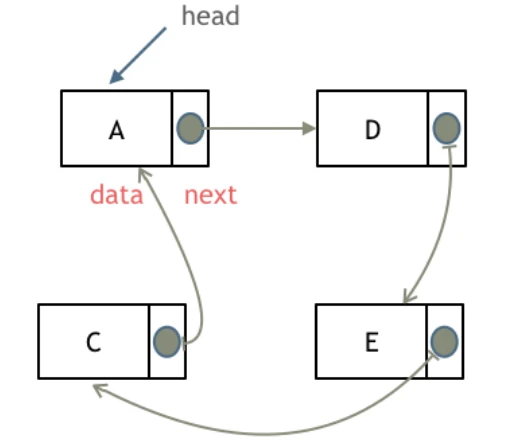
链表的存储方式
了解完链表的类型,再来说一说链表在内存中的存储方式。
数组是在内存中是连续分布的,但是链表在内存中可不是连续分布的。
链表是通过指针域的指针链接在内存中各个节点。
所以链表中的节点在内存中不是连续分布的 ,而是散乱分布在内存中的某地址上,分配机制取决于操作系统的内存管理。
如图所示:
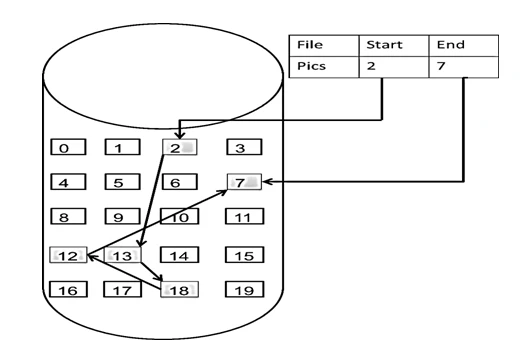
这个链表起始节点为2, 终止节点为7, 各个节点分布在内存的不同地址空间上,通过指针串联在一起。
链表的定义
平时在刷leetcode的时候,链表的节点都默认定义好了,直接用就行了
而在面试的时候,一旦要自己手写链表,如果不定义构造函数使用默认构造函数的话,在初始化的时候就不能直接给变量赋值!
public class ListNode {
// 结点的值
int val;
// 下一个结点
ListNode next;
// 节点的构造函数(无参)
public ListNode() {
}
// 节点的构造函数(有一个参数)
public ListNode(int val) {
this.val = val;
}
// 节点的构造函数(有两个参数)
public ListNode(int val, ListNode next) {
this.val = val;
this.next = next;
}
}
链表的操作
删除节点
删除D节点,如图所示:
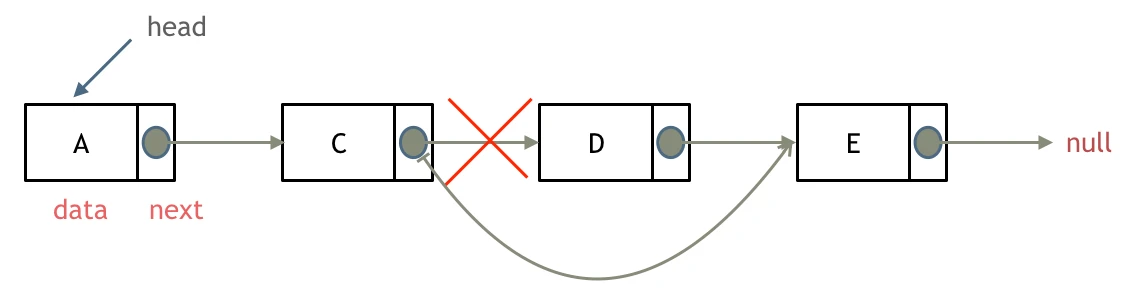
只要将C节点的next指针 指向E节点就可以了。
那有同学说了,D节点不是依然存留在内存里么?只不过是没有在这个链表里而已。
是这样的,所以在C++里最好是再手动释放这个D节点,释放这块内存。
其他语言例如Java、Python,就有自己的内存回收机制,就不用自己手动释放了。
添加节点
如图所示:
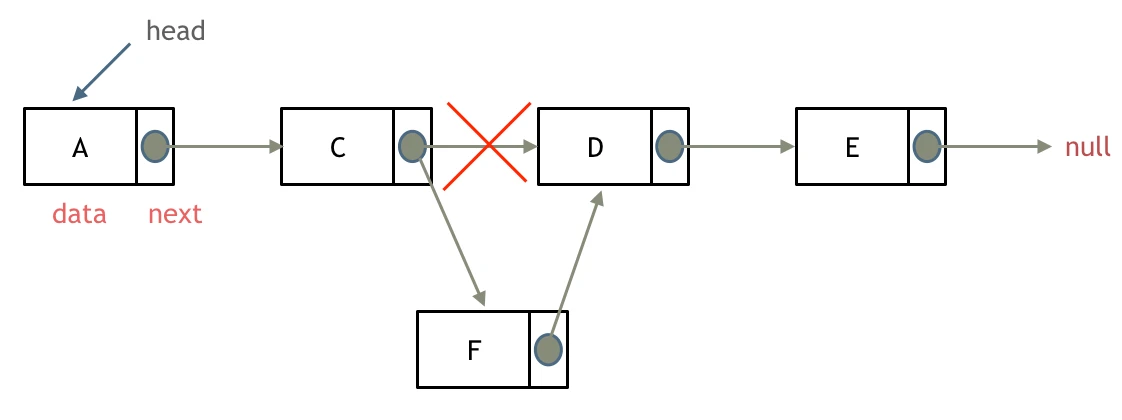
可以看出链表的增添和删除都是O(1)操作,也不会影响到其他节点。
但是要注意,要是删除第五个节点,需要从头节点查找到第四个节点通过next指针进行删除操作,查找的时间复杂度是O(n)。
性能分析
再把链表的特性和数组的特性进行一个对比,如图所示:
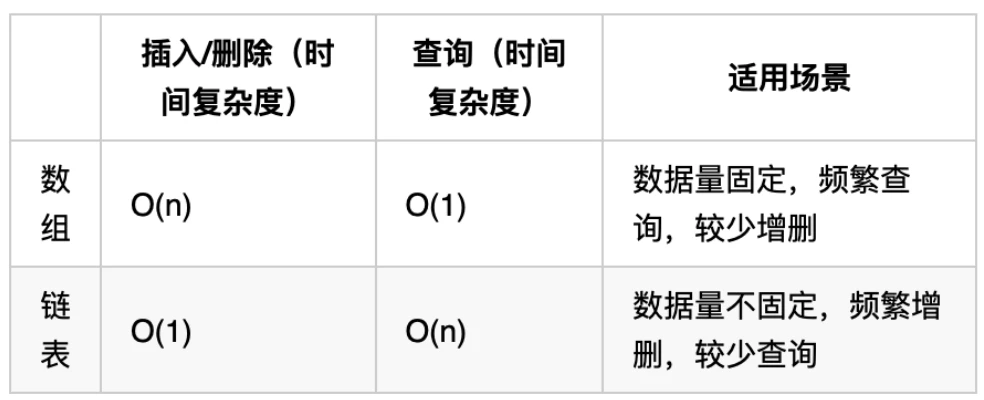
数组在定义的时候,长度就是固定的,如果想改动数组的长度,就需要重新定义一个新的数组。
链表的长度可以是不固定的,并且可以动态增删, 适合数据量不固定,频繁增删,较少查询的场景。
哈希表
首先什么是 哈希表,哈希表(英文名字为Hash table,国内也有一些算法书籍翻译为散列表,大家看到这两个名称知道都是指hash table就可以了)。
哈希表是根据关键码的值而直接进行访问的数据结构。
这么这官方的解释可能有点懵,其实直白来讲其实数组就是一张哈希表。
哈希表中关键码就是数组的索引下标,然后通过下标直接访问数组中的元素,如下图所示:
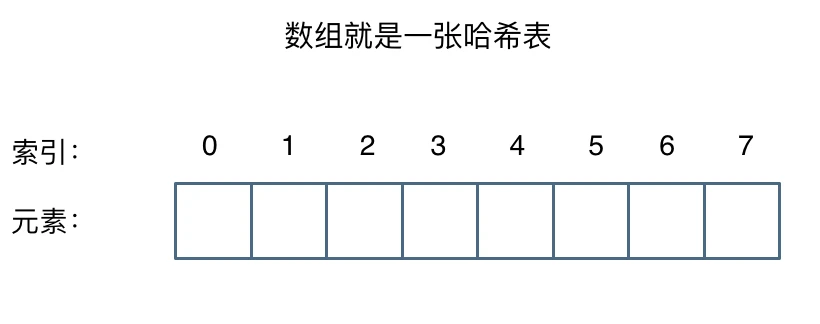
那么哈希表能解决什么问题呢,一般哈希表都是用来快速判断一个元素是否出现集合里。
例如要查询一个名字是否在这所学校里。
要枚举的话时间复杂度是O(n),但如果使用哈希表的话, 只需要O(1)就可以做到。
我们只需要初始化把这所学校里学生的名字都存在哈希表里,在查询的时候通过索引直接就可以知道这位同学在不在这所学校里了。
将学生姓名映射到哈希表上就涉及到了hash function ,也就是哈希函数。
哈希函数
哈希函数,把学生的姓名直接映射为哈希表上的索引,然后就可以通过查询索引下标快速知道这位同学是否在这所学校里了。
哈希函数如下图所示,通过hashCode把名字转化为数值,一般hashcode是通过特定编码方式,可以将其他数据格式转化为不同的数值,这样就把学生名字映射为哈希表上的索引数字了。
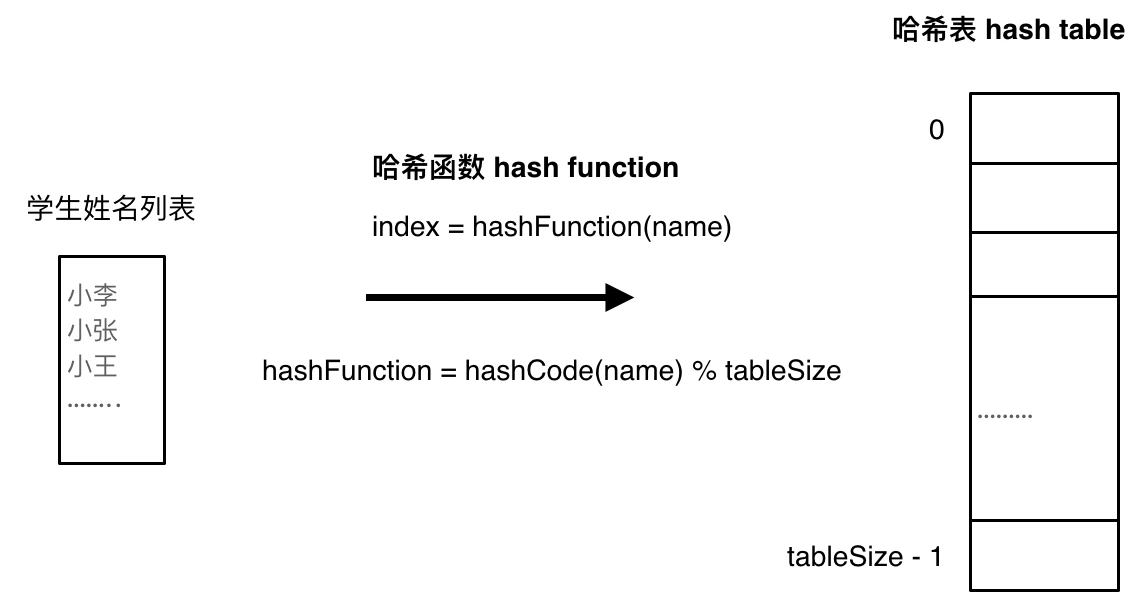
如果hashCode得到的数值大于 哈希表的大小了,也就是大于tableSize了,怎么办呢?
此时为了保证映射出来的索引数值都落在哈希表上,我们会在再次对数值做一个取模的操作,就要我们就保证了学生姓名一定可以映射到哈希表上了。
此时问题又来了,哈希表我们刚刚说过,就是一个数组。
如果学生的数量大于哈希表的大小怎么办,此时就算哈希函数计算的再均匀,也避免不了会有几位学生的名字同时映射到哈希表 同一个索引下标的位置。
接下来哈希碰撞登场
哈希碰撞
如图所示,小李和小王都映射到了索引下标 1 的位置,这一现象叫做哈希碰撞。
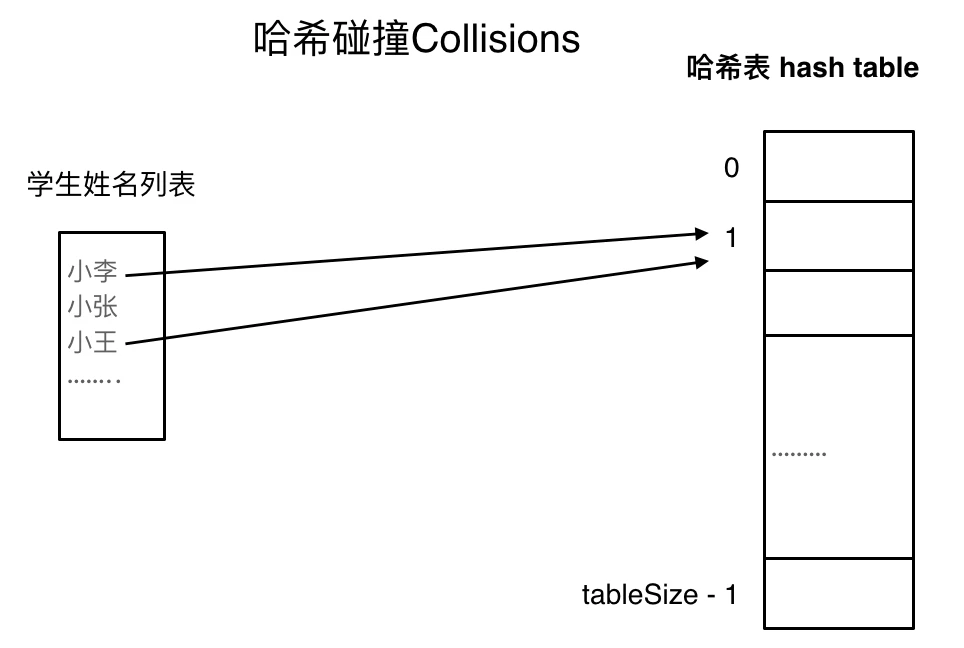
一般哈希碰撞有两种解决方法, 拉链法和线性探测法。
拉链法
刚刚小李和小王在索引1的位置发生了冲突,发生冲突的元素都被存储在链表中。 这样我们就可以通过索引找到小李和小王了
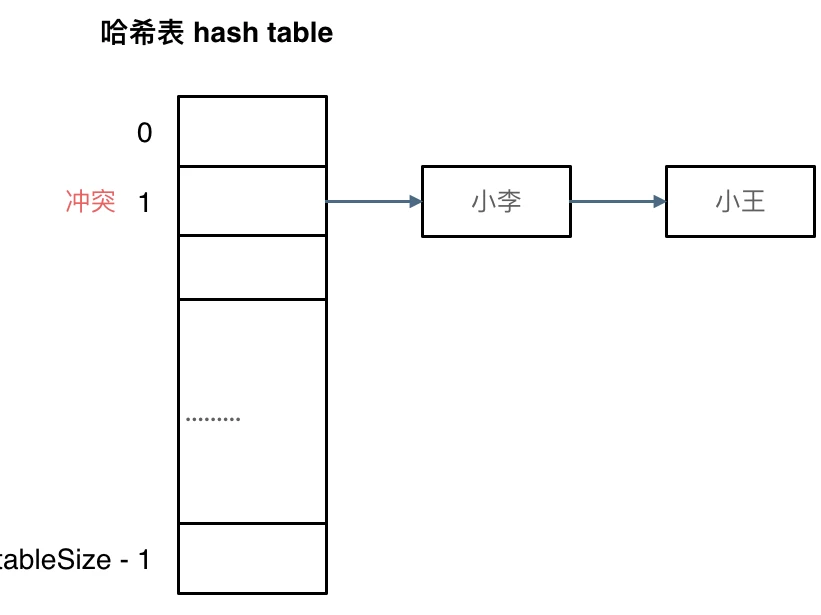
(数据规模是dataSize, 哈希表的大小为tableSize)
其实拉链法就是要选择适当的哈希表的大小,这样既不会因为数组空值而浪费大量内存,也不会因为链表太长而在查找上浪费太多时间。
线性探测法
使用线性探测法,一定要保证tableSize大于dataSize。 我们需要依靠哈希表中的空位来解决碰撞问题。
例如冲突的位置,放了小李,那么就向下找一个空位放置小王的信息。所以要求tableSize一定要大于dataSize ,要不然哈希表上就没有空置的位置来存放 冲突的数据了。如图所示:
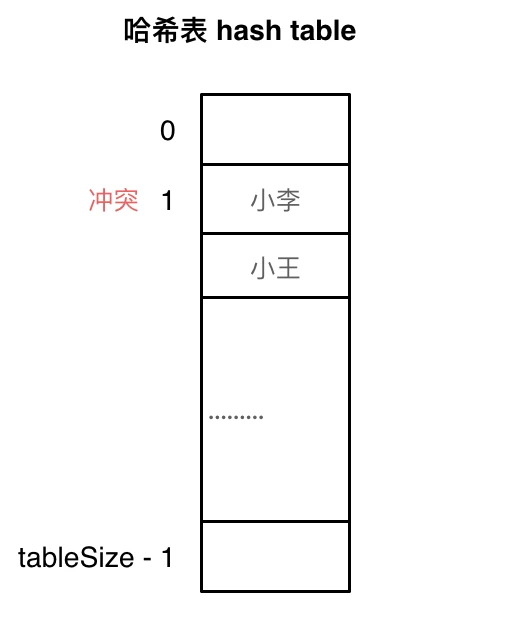
其实关于哈希碰撞还有非常多的细节,感兴趣的同学可以再好好研究一下,这里我就不再赘述了。
常见的三种哈希结构
当我们想使用哈希法来解决问题的时候,我们一般会选择如下三种数据结构。
- 数组
- set (集合)
- map(映射)
这里数组就没啥可说的了,我们来看一下set。
在C++中,set 和 map 分别提供以下三种数据结构,其底层实现以及优劣如下表所示:
| 集合 | 底层实现 | 是否有序 | 数值是否可以重复 | 能否更改数值 | 查询效率 | 增删效率 |
|---|---|---|---|---|---|---|
| std::set | 红黑树 | 有序 | 否 | 否 | O(log n) | O(log n) |
| std::multiset | 红黑树 | 有序 | 是 | 否 | O(logn) | O(logn) |
| std::unordered_set | 哈希表 | 无序 | 否 | 否 | O(1) | O(1) |
std::unordered_set底层实现为哈希表,std::set 和std::multiset 的底层实现是红黑树,红黑树是一种平衡二叉搜索树,所以key值是有序的,但key不可以修改,改动key值会导致整棵树的错乱,所以只能删除和增加。
| 映射 | 底层实现 | 是否有序 | 数值是否可以重复 | 能否更改数值 | 查询效率 | 增删效率 |
|---|---|---|---|---|---|---|
| std::map | 红黑树 | key有序 | key不可重复 | key不可修改 | O(logn) | O(logn) |
| std::multimap | 红黑树 | key有序 | key可重复 | key不可修改 | O(log n) | O(log n) |
| std::unordered_map | 哈希表 | key无序 | key不可重复 | key不可修改 | O(1) | O(1) |
std::unordered_map 底层实现为哈希表,std::map 和std::multimap 的底层实现是红黑树。同理,std::map 和std::multimap 的key也是有序的(这个问题也经常作为面试题,考察对语言容器底层的理解)。
当我们要使用集合来解决哈希问题的时候,优先使用unordered_set,因为它的查询和增删效率是最优的,如果需要集合是有序的,那么就用set,如果要求不仅有序还要有重复数据的话,那么就用multiset。
那么再来看一下map ,在map 是一个key value 的数据结构,map中,对key是有限制,对value没有限制的,因为key的存储方式使用红黑树实现的。
其他语言例如:java里的HashMap ,TreeMap 都是一样的原理。可以灵活贯通。
虽然std::set、std::multiset 的底层实现是红黑树,不是哈希表,std::set、std::multiset 使用红黑树来索引和存储,不过给我们的使用方式,还是哈希法的使用方式,即key和value。所以使用这些数据结构来解决映射问题的方法,我们依然称之为哈希法。 map也是一样的道理。
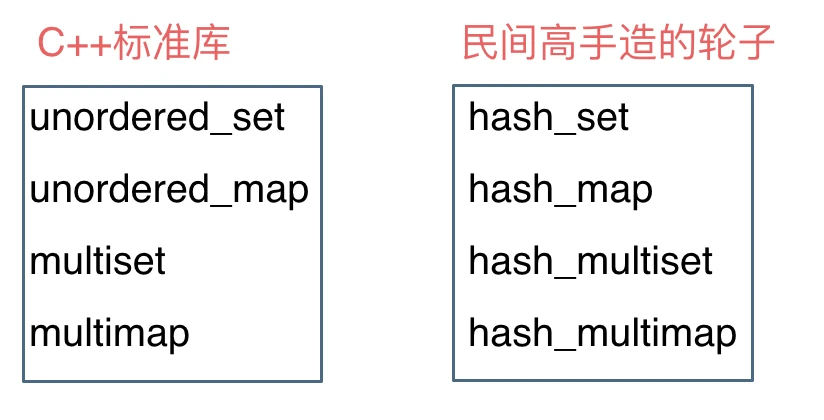
这里在说一下,一些C++的经典书籍上 例如STL源码剖析,说到了hash_set hash_map,这个与unordered_set,unordered_map又有什么关系呢?
实际上功能都是一样一样的, 但是unordered_set在C++11的时候被引入标准库了,而hash_set并没有,所以建议还是使用unordered_set比较好,这就好比一个是官方认证的,hash_set,hash_map 是C++11标准之前民间高手自发造的轮子。
总结
总结一下,当我们遇到了要快速判断一个元素是否出现集合里的时候,就要考虑哈希法。
但是哈希法也是牺牲了空间换取了时间,因为我们要使用额外的数组,set或者是map来存放数据,才能实现快速的查找。
如果在做面试题目的时候遇到需要判断一个元素是否出现过的场景也应该第一时间想到哈希法!
字符串
字符串是若干字符组成的有限序列,也可以理解为是一个字符数组,但是很多语言对字符串做了特殊的规定。
字符串类类型的题目,往往想法比较简单,但是实现起来并不容易,复杂的字符串题目非常考验对代码的掌控能力。
双指针法是字符串处理的常客。
全局反转和局部反转的魔力~
KMP算法是字符串查找最重要的算法,但彻底理解KMP并不容易,我们已经写了五篇KMP的文章,不断总结和完善,最终才把KMP讲清楚。
栈和队列
来看看栈和队列不为人知的一面
我想栈和队列的原理大家应该很熟悉了,队列是先进先出,栈是先进后出。
如图所示:
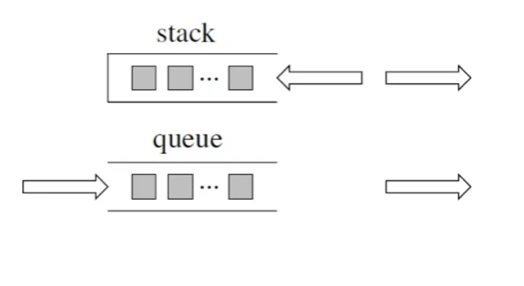
那么关于栈的问题,栈是容器吗?
有的同学可能仅仅知道有栈和队列这么个数据结构,却不知道底层实现,也不清楚所使用栈和队列和STL是什么关系。
所以这里我再给大家扫一遍基础知识,
首先大家要知道 栈和队列是STL(C++标准库)里面的两个数据结构。
C++标准库是有多个版本的,要知道我们使用的STL是哪个版本,才能知道对应的栈和队列的实现原理。
那么来介绍一下,三个最为普遍的STL版本:
- HP STL 其他版本的C++ STL,一般是以HP STL为蓝本实现出来的,HP STL是C++ STL的第一个实现版本,而且开放源代码。
- P.J.Plauger STL 由P.J.Plauger参照HP STL实现出来的,被Visual C++编译器所采用,不是开源的。
- SGI STL 由Silicon Graphics Computer Systems公司参照HP STL实现,被Linux的C++编译器GCC所采用,SGI STL是开源软件,源码可读性甚高。
接下来介绍的栈和队列也是SGI STL里面的数据结构, 知道了使用版本,才知道对应的底层实现。
来说一说栈,栈先进后出,如图所示:
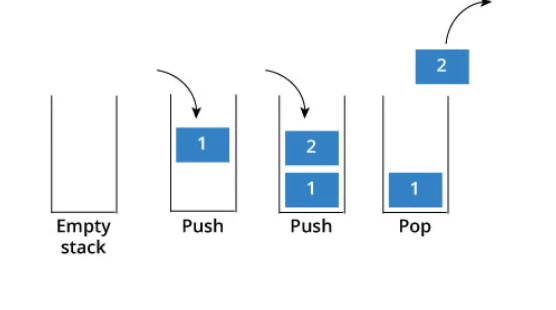
栈提供push 和 pop 等等接口,所有元素必须符合先进后出规则,所以栈不提供走访功能,也不提供迭代器(iterator)。 不像是set 或者map 提供迭代器iterator来遍历所有元素。
栈是以底层容器完成其所有的工作,对外提供统一的接口,底层容器是可插拔的(也就是说我们可以控制使用哪种容器来实现栈的功能)。
所以STL中栈往往不被归类为容器,而被归类为container adapter(容器适配器)。
那么问题来了,STL 中栈是用什么容器实现的?
从下图中可以看出,栈的内部结构,栈的底层实现可以是vector,deque,list 都是可以的, 主要就是数组和链表的底层实现。
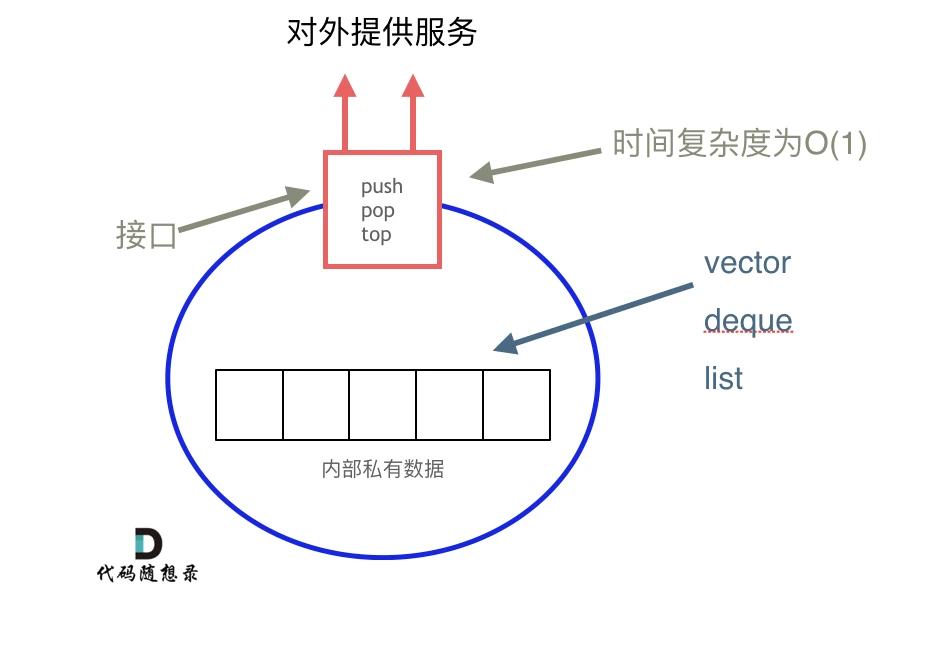 所以,栈和队列不是容器,而是容器适配器
所以,栈和队列不是容器,而是容器适配器
树
树的种类
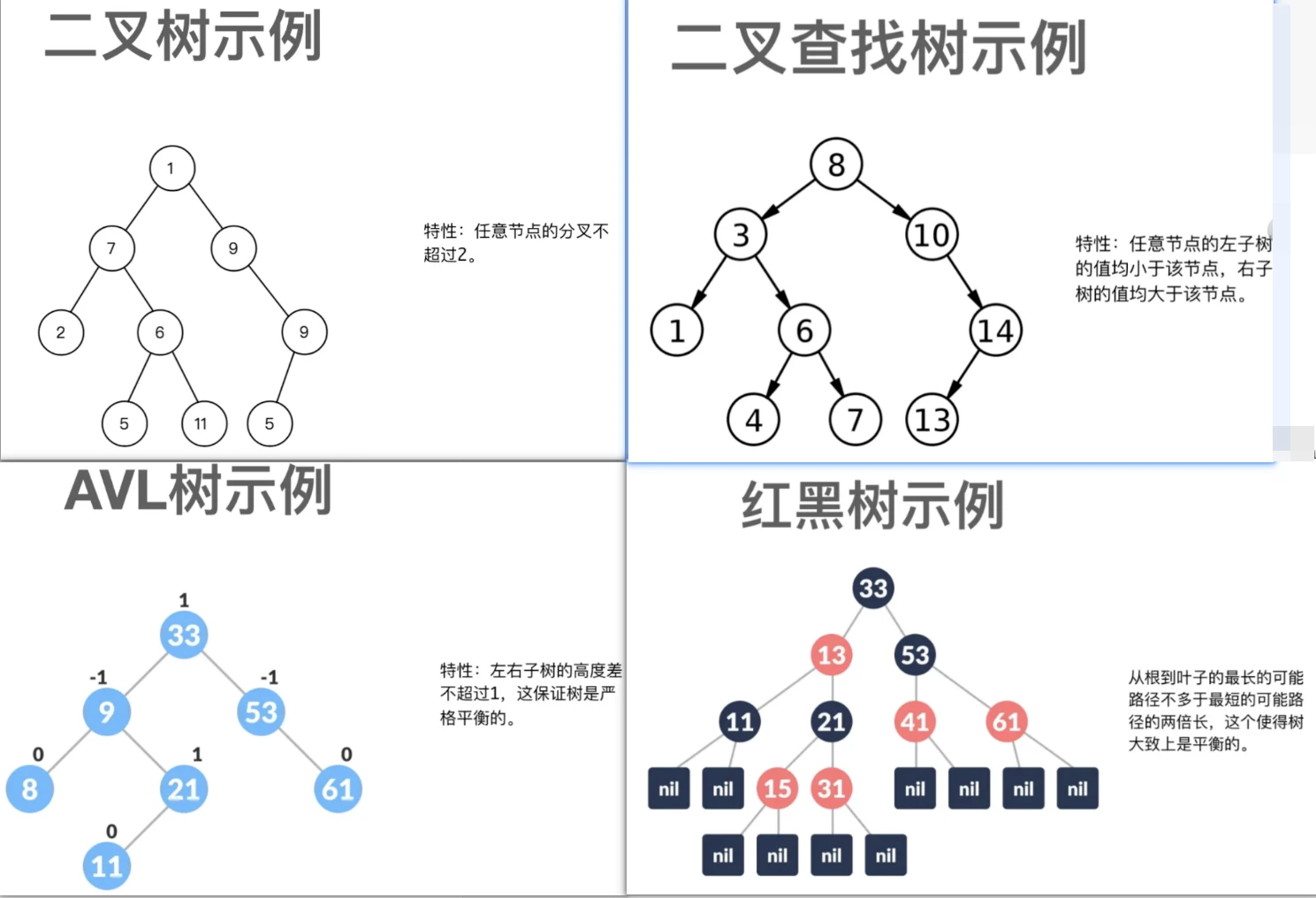
树的种类很多,包括二叉树、二叉查找树、AVL树、红黑树、B树、B+树等。它们有各自的应用场景。
- 二叉树,顾名思义,就是有两个子树的树数据结构。
- 二叉查找树要求左子树的值均小于根节点,右子树的值均大于于根节点的值。
二叉查找树在最坏的情况下就是会退化成一个有n个节点的线性链表。 - 在二叉查找树的基础上,进一步做限制,这也就出现了AVL树(严格平衡的二叉查找树,要求左右子树树高不超过1)、红黑树(弱平衡二叉树,效率较AVL树高,常用于实现关联数组dict)。
B树和B+树都是多叉树,常用于操作系统的文件索引和数据库索引。
可见二叉树只是树的一个简单形式,但是二叉树在树结构中有非常重要的地位,二叉树的许多操作都可以泛化至其他类型的树上。从出题的角度而言,二叉树的频率也是最高的。
树的遍历
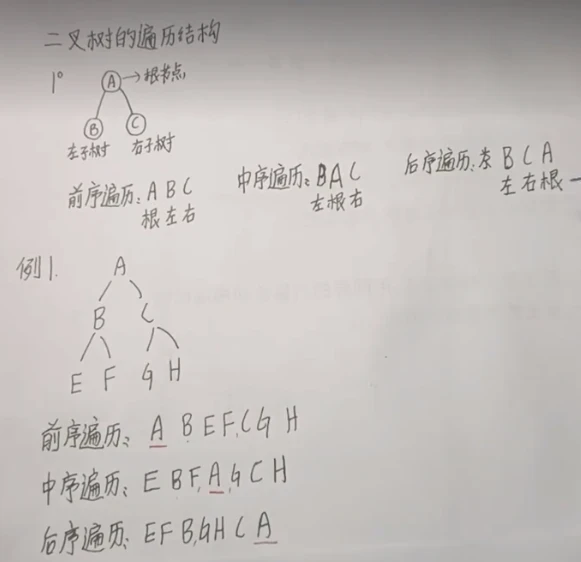
树的遍历其实就两种:广度和深度
深度优先
前序、中序和后序遍历是树的深度优先遍历(Depth-First Traversal)的三个不同变种,它们属于树的深度(Depth)方面的遍历策略。这三种遍历方式都是沿着树的深度方向进行,即从根节点开始,一直深入到叶节点,然后再回溯。
- 前:根左右
- 中:左根右
- 后:左右根
广度优先
首先访问树的底层节点,然后逐层向上遍历,直到所有层的所有节点都被访问过。广度优先遍历通常使用队列来实现。
参考题目:102. 二叉树的层序遍历 - 力扣(LeetCode),依次输出每一层的元素都是谁
迭代实现
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
Queue<TreeNode> queue = new LinkedList<>();
List<List<Integer>> res = new ArrayList<>();
if (root != null) queue.add(root);
while (!queue.isEmpty()) {
List<Integer> tmp = new ArrayList<>();
for(int i = queue.size(); i > 0; i--) {
TreeNode node = queue.poll();
tmp.add(node.val);
if (node.left != null) queue.add(node.left);
if (node.right != null) queue.add(node.right);
}
res.add(tmp);
}
return res;
}
}
递归实现
class Solution {
List<List<Integer>> list = new ArrayList<>();
public List<List<Integer>> levelOrder(TreeNode root) {
dns(root,0);
return list;
}
public void dns(TreeNode node,int lever){
if(node == null) return;
if(list.size()==lever) list.add(new ArrayList<Integer>());
list.get(lever).add(node.val);
dns(node.left,lever+1);
dns(node.right,lever+1);
}
}
树节点的度
树是一种特殊的图,度是相对于树节点而言的概念
树的“度”通常指的是树中任意节点的子节点数
树中节点的度描述如下:
- 根节点的度为0或1(如果它有一个子节点)。
- 内部节点的度至少为1(它们有至少一个子节点)。
- 叶子节点的度为0(它们没有子节点)。
二叉树的种类
在我们解题过程中二叉树有两种主要的形式:满二叉树和完全二叉树。
满二叉树
满二叉树:如果一棵二叉树只有度为0的结点和度为2的结点,并且度为0的结点在同一层上,则这棵二叉树为满二叉树。
如图所示:
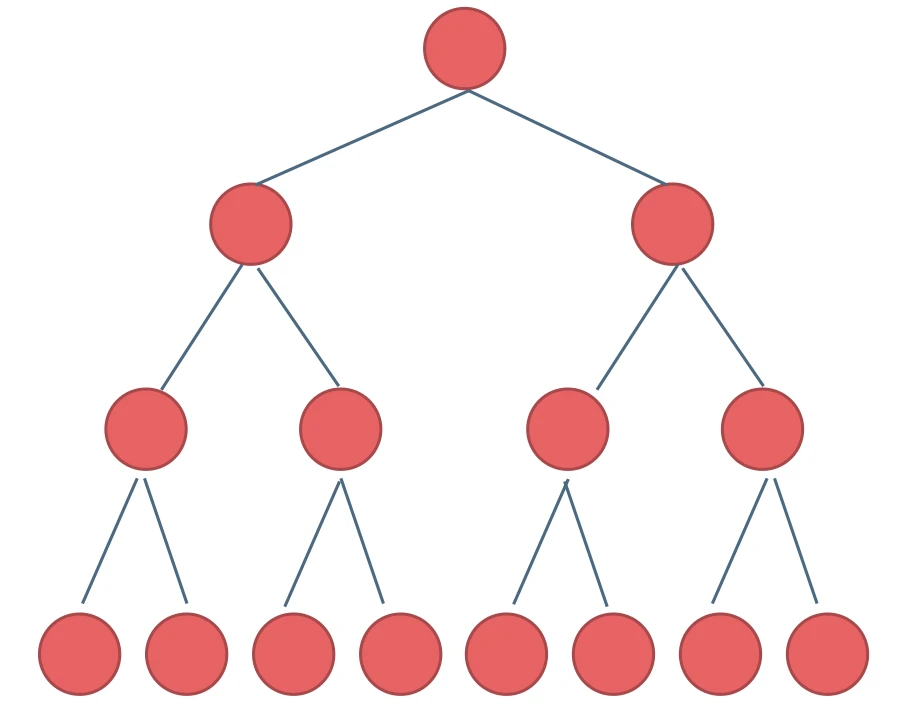
这棵二叉树为满二叉树,也可以说深度为k,有2^k-1个节点的二叉树。
完全二叉树
什么是完全二叉树?
完全二叉树的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2^(h-1) 个节点。
大家要自己看完全二叉树的定义,很多同学对完全二叉树其实不是真正的懂了。
我来举一个典型的例子如题:
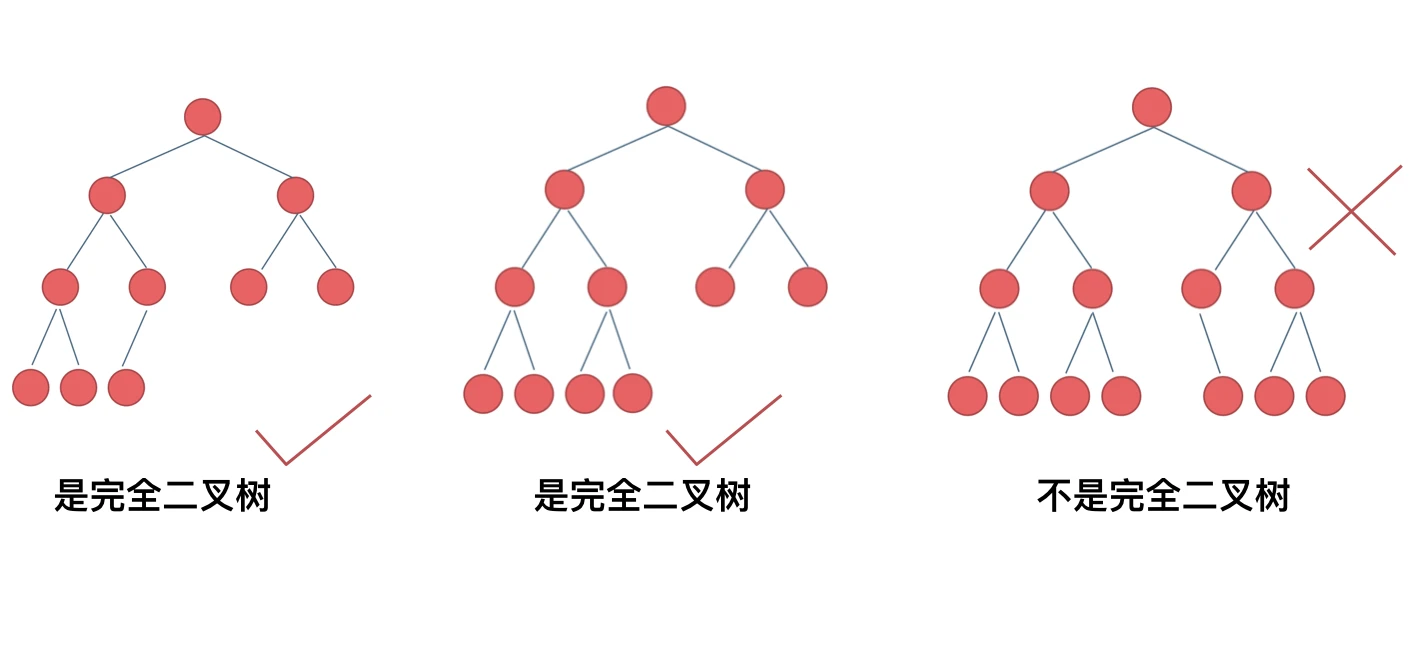
相信不少同学最后一个二叉树是不是完全二叉树都中招了。
之前我们刚刚讲过优先级队列其实是一个堆,堆就是一棵完全二叉树,同时保证父子节点的顺序关系。
二叉搜索树
前面介绍的树,都没有数值的,而二叉搜索树是有数值的了,二叉搜索树是一个有序树。
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 它的左、右子树也分别为二叉排序树
下面这两棵树都是搜索树 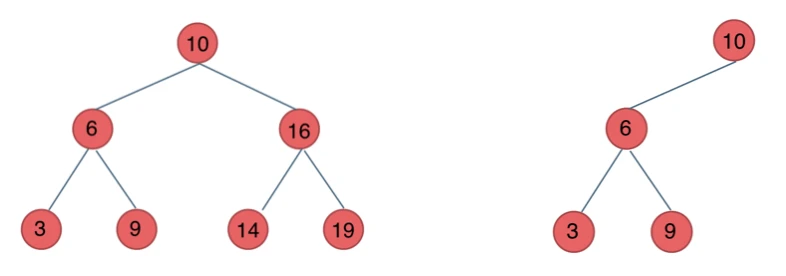
平衡二叉搜索树
平衡二叉搜索树:又被称为AVL(Adelson-Velsky and Landis)树,且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
如图:
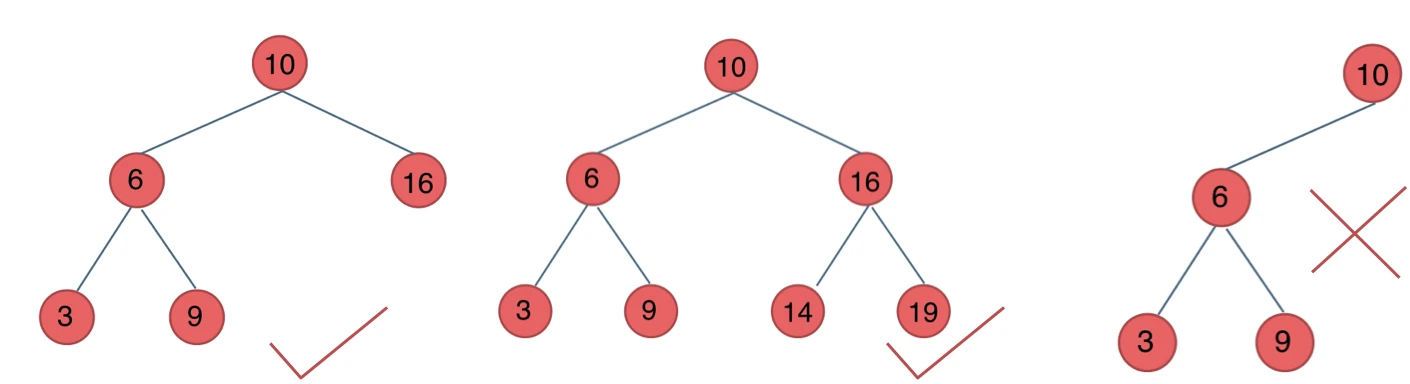
最后一棵 不是平衡二叉树,因为它的左右两个子树的高度差的绝对值超过了1。
C++中map、set、multimap,multiset的底层实现都是平衡二叉搜索树,所以map、set的增删操作时间时间复杂度是logn,注意我这里没有说unordered_map、unordered_set,unordered_map、unordered_set底层实现是哈希表。
所以大家使用自己熟悉的编程语言写算法,一定要知道常用的容器底层都是如何实现的,最基本的就是map、set等等,否则自己写的代码,自己对其性能分析都分析不清楚!
二叉树的存储方式
二叉树可以链式存储,也可以顺序存储。
那么链式存储方式就用指针, 顺序存储的方式就是用数组。
顾名思义就是顺序存储的元素在内存是连续分布的,而链式存储则是通过指针把分布在各个地址的节点串联一起。
链式存储如图:
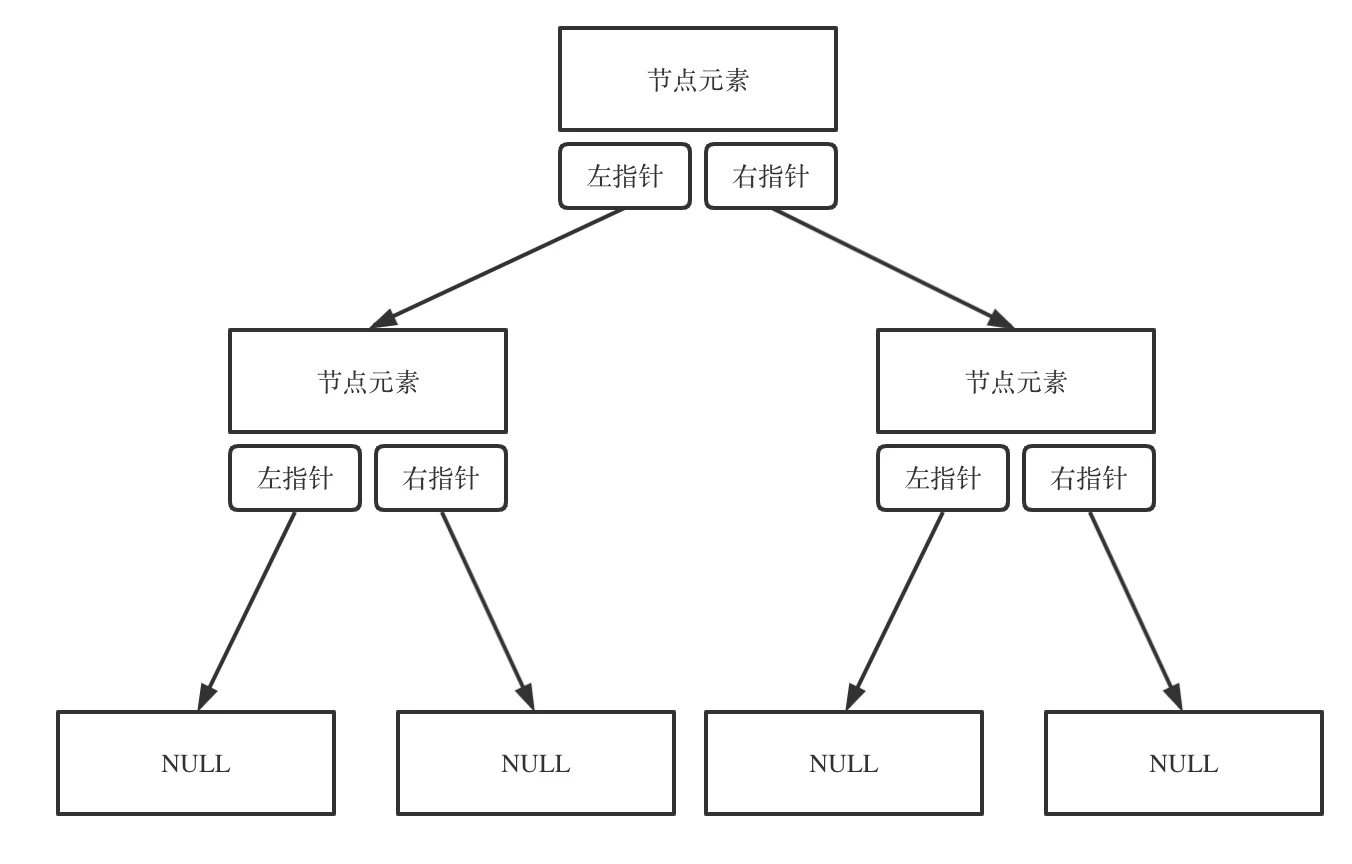
链式存储是大家很熟悉的一种方式,那么我们来看看如何顺序存储呢?
其实就是用数组来存储二叉树,顺序存储的方式如图:
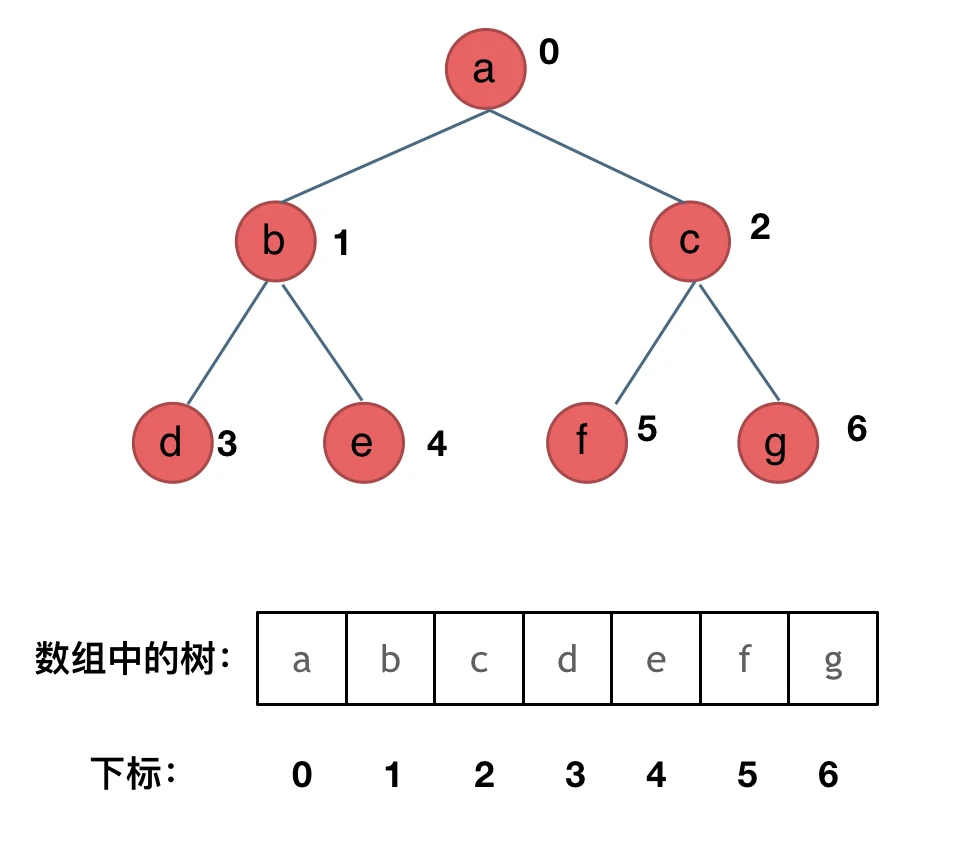
用数组来存储二叉树如何遍历的呢?
如果父节点的数组下标是 i,那么它的左孩子就是 i *2 + 1,右孩子就是 i* 2 + 2。
但是用链式表示的二叉树,更有利于我们理解,所以一般我们都是用链式存储二叉树。
所以大家要了解,用数组依然可以表示二叉树。
二叉树的遍历方式
关于二叉树的遍历方式,要知道二叉树遍历的基本方式都有哪些。
一些同学用做了很多二叉树的题目了,可能知道前中后序遍历,可能知道层序遍历,但是却没有框架。
我这里把二叉树的几种遍历方式列出来,大家就可以一一串起来了。
二叉树主要有两种遍历方式:
- 深度优先遍历:先往深走,遇到叶子节点再往回走。
- 广度优先遍历:一层一层的去遍历。
这两种遍历是图论中最基本的两种遍历方式,后面在介绍图论的时候 还会介绍到。
那么从深度优先遍历和广度优先遍历进一步拓展,才有如下遍历方式:
- 深度优先遍历
- 前序遍历(递归法,迭代法)
- 中序遍历(递归法,迭代法)
- 后序遍历(递归法,迭代法)
- 广度优先遍历
- 层次遍历(迭代法)
在深度优先遍历中:有三个顺序,前中后序遍历, 有同学总分不清这三个顺序,经常搞混,我这里教大家一个技巧。
这里前中后,其实指的就是中间节点的遍历顺序,只要大家记住 前中后序指的就是中间节点的位置就可以了。
看如下中间节点的顺序,就可以发现,中间节点的顺序就是所谓的遍历方式
- 前序遍历:中左右
- 中序遍历:左中右
- 后序遍历:左右中
大家可以对着如下图,看看自己理解的前后中序有没有问题。
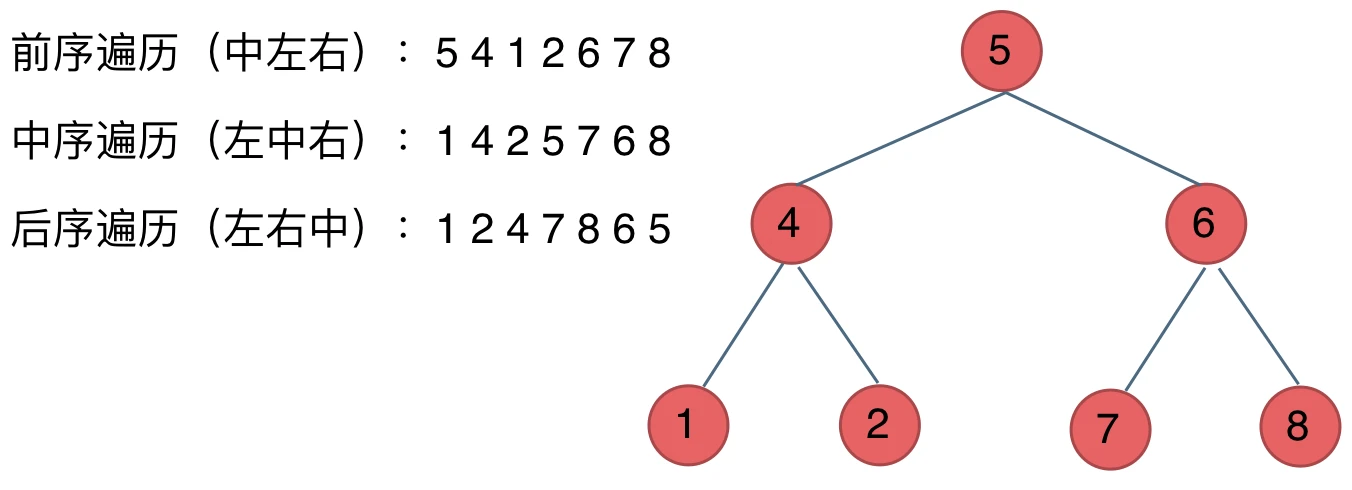
最后再说一说二叉树中深度优先和广度优先遍历实现方式,我们做二叉树相关题目,经常会使用递归的方式来实现深度优先遍历,也就是实现前中后序遍历,使用递归是比较方便的。
之前我们讲栈与队列的时候,就说过栈其实就是递归的一种实现结构,也就说前中后序遍历的逻辑其实都是可以借助栈使用非递归的方式来实现的。
而广度优先遍历的实现一般使用队列来实现,这也是队列先进先出的特点所决定的,因为需要先进先出的结构,才能一层一层的来遍历二叉树。
这里其实我们又了解了栈与队列的一个应用场景了。
具体的实现我们后面都会讲的,这里大家先要清楚这些理论基础。
二叉树的定义
刚刚我们说过了二叉树有两种存储方式顺序存储,和链式存储,顺序存储就是用数组来存,这个定义没啥可说的,我们来看看链式存储的二叉树节点的定义方式。
C++代码如下:
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) { this.val = val; }
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
大家会发现二叉树的定义 和链表是差不多的,相对于链表 ,二叉树的节点里多了一个指针, 有两个指针,指向左右孩子。
这里要提醒大家要注意二叉树节点定义的书写方式。
在现场面试的时候 面试官可能要求手写代码,所以数据结构的定义以及简单逻辑的代码一定要锻炼白纸写出来。
因为我们在刷leetcode的时候,节点的定义默认都定义好了,真到面试的时候,需要自己写节点定义的时候,有时候会一脸懵逼!
总结-题型
二叉树是一种基础数据结构,在算法面试中都是常客,也是众多数据结构的基石。
说到二叉树,就不得不说递归,很多同学对递归都是又熟悉又陌生,递归的代码一般很简短,但每次都是一看就会,一写就废。
题目分类大纲如下:
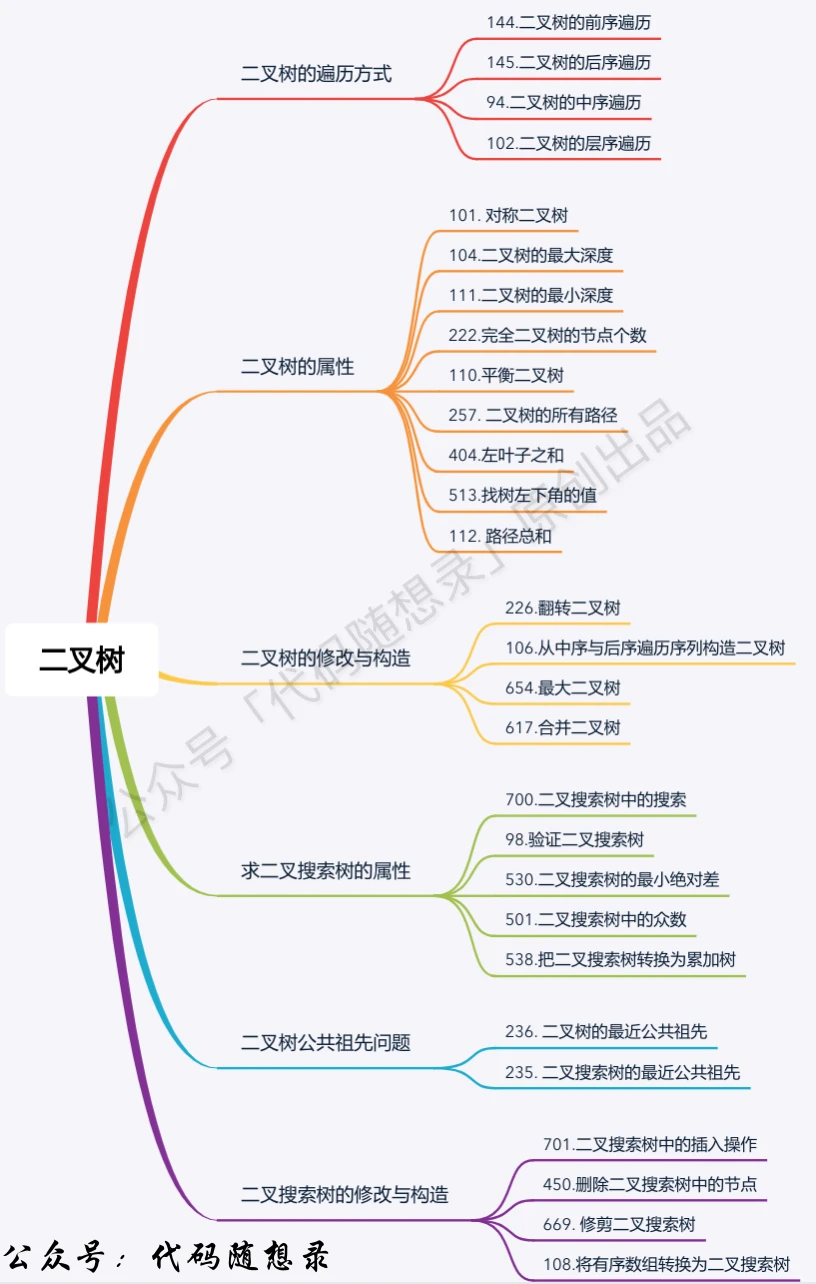
图

在图论中,“度”指的是图中一个节点的邻接节点数,即与该节点直接相连的边的数量。一个节点的度可以是任何非负整数。如果一个节点的度为k,那么它与k个其他节点直接相连。
按照定义,图分为有向图和无向图,图论中还有入度、出度的概念
图的存储结构
邻接矩阵


邻接表